|
ssmkit
master-68aed98
|
|
ssmkit
master-68aed98
|
In this tutorial we show how ssmkit can be used for simulating and state estimation (tracking) of a constant velocity inertial model. This is a classical application in the state space models. The tutorial is written for basic and advanced users. The code for this tutorial can be found in /example/tutorial_constant_velocity.cpp.
Let \(\mathbf{x}_k = [x_1(k), x_2(k), \dot{x}_1(k), \dot{x}_2(k)]^T \) be the state of an object at time \(k\) moving in a 2D space, where \(x_1(k)\) and \(\dot{x}_1(k)\) are the position and velocity in the first dimension and \(x_2(k)\) and \(\dot{x}_2(k)\) are position and velocity in the second dimension. The dynamic of this state vector can be formulated as
\[\mathbf{x}_k = \mathbf{F}\mathbf{x}_{k-1} + \boldsymbol\omega_k \]
Where \(\mathbf{F}\) is refered to as transition or dynamic matrix. It is defined as
\[ \mathbf{F} = \begin{bmatrix} 1 & 0 & \delta & 0 \\ 0 & 1 & 0 & \delta \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
for sampling rate of \(\delta\) second. \(\boldsymbol\omega\) is a zero-mean white Gaussian random process with covariance matrix \(\mathbf{Q}\).
The \(\boldsymbol\omega\) is introduced to model our uncertainty about the deterministic dynamic model \(\mathbf{F}\).
In real application often access to the object's state is only available through a noisy measurement process:
\begin{equation} \mathbf{z}_k = \mathbf{H}\mathbf{x}_k+\boldsymbol\nu \end{equation}
wher \(\mathbf{z}_k\) is measurement vector at time \(k\). \(\boldsymbol\nu\) is a zero-mean white Gaussian random process with covariance matrix \(\mathbf{R}\) and \(\mathbf{H}\) is called measurement matrix whichi, for our purpose, is defined as:
\[ \mathbf{H} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \]
Our measurement process simply mean that the measurment vector is the position of the object plus a Gaussian noise.
Unlike \(\boldsymbol\omega\), the purpose of \(\boldsymbol\nu\) is to model imperfection related to the measurement device.
The dynamic and measurement equations can easily be interepreted as conditional probability distribution functions (CPDF):
\[ p(\mathbf{x}_k|\mathbf{x}_{k-1}) = \mathcal{N}(\mathbf{F}\mathbf{x}_{k-1}, \mathbf{Q}) \]
\[ p(\mathbf{z}_k|\mathbf{x}_{k}) = \mathcal{N}(\mathbf{H}\mathbf{x}_{k}, \mathbf{R}) \]
where \(\mathcal{N}(\mu,\Sigma)\) is a Gaussian distribution with mean \(\mu\) and covariance \(\Sigma\). Let also assume that the initial state probability distribution function is a Gaussian:
\[ p(\mathbf{x}_0) = \mathcal{N}(\hat{\mathbf{x}}_0, \mathbf{P}_0) \]
These probability density functions fully characterize a stochastic process that can be represented by a two-layer hierarchical dynamic Bayesian network (DBN) of this form
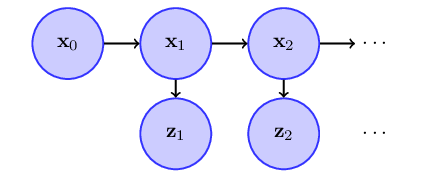
The first layer of this process is a first-order Markov process where the state at each time instance is only dependent on the state at previous time instant. The second layer in an independent or memoryless process where the values of the process at previous time instances do not have any effect on the value of next time instances.
The same intuition used in mathematical construction of the stochastic processes is used in ssmkit for constructing process objects. In ssmkit process objects are realizations of stochastic processes which are representable as DBN. A DBN is a graphical model that shows statistical dependencies betveen random variables represented as CPDF. In the next sections We will see how we can define CPDFs in ssmkit and use them to construct simple processes which are later combined to make more complex processes.
We start by defining the parameters of the system:
arma::mat and arma::vec are matrix and vector data-types from armadillo library. This is the core linear algebra library used by ssmkit.
we define initial state PDF \(p(\mathbf{x}_0)\) using ssmkit::distribution::Gaussian class:
the class ssmkit::distribution::Gaussian implements a multivariate Gaussian distribution and can be used for sampling and calculating likelihood of random variables. Note that we passed mean vector and covariance matrix we defined above to its constructor.
We now turn to the definition of the state transition CPDF and the measurement CPDF. Before that it is important to understand how CPDFs are treated in ssmkit. CPDFs are defined as a combination of a parametric PDF and a parameter map. In other words \(p(x|y) = \mathcal{F}(g(y))\) where \(\mathcal{F}(\theta)\) is parametric distribution (e.g. Gaussian) with parameter Set \(\theta\) and \(g(y) = \theta\) maps the condition variable \(y\) to a parameter \(\theta\). The parameter set of Gaussian is a tuple \((\mu, \Sigma)\) of mean vector and covariance matrix. Thus, for our purpose the function \(g\) should receive a state variable \(\mathbf{x}\) and return \((\mathbf{F}\mathbf{x}, \mathbf{Q})\) for transition CPDF and \((\mathbf{H}\mathbf{x}, \mathbf{R})\) for measurement CPDF. This special kind of parameter map is implemented in class ssmkit::map::LinearGaussian(trans, cov) which is constructed using a linear transformation matrix trans and a covariance matrix cov. Note that it always return the same covariance matrix which is constructed with.
The class ssmkit::distribution::Conditional provides a generic class that constructs a conditional distribution form a parametric distribution and a parameter map. We can make any kind of CPDF with this class.
The two CPDFs are constructed by:
we used ssmkit::distribution::makeConditional function for constructing CPDFs. This is a convenient interface to the class constructor that does not require ugly template arguments. ssmkit::distribution::Gaussian(dim) is another constructor for Gaussian PDF object with dimensions dim. Note that we pass the PDF object to Conditional in order to let it know what type of distribution we need. Internal to CPDF object, the parameters of distribution are actually come from the parameter map object.
Now that we have the CPDFs we start constructing the hierarchical process. First, let build each layer separately:
The function ssmkit::process::makeMarkov() receives an initial PDF and a CPDFs and construct a Markovian random process of class ssmkit::process::Markov. The function ssmkit::process::makeMemoryless() takes a CPDFs and returns a memoryless or independent random process of class ssmkit::process::Memoryless.
Finally, we can use the class ssmkit::process::Hierarchical to construct SSM process.
The function ssmkit::process::makeHierarchical() takes an arbitrary number of processes and construct a process of class ssmkit::process::Hierarchical. Hierarchical processes are built by stacking other processes on top of each other. The Hierarchical class connects the random variable of a process to the condition variable of the process in the lower level.
No we have our process object. If it looks too long you may write all in one statement:
The objects of process class provide three basic methods: initialize, random and likelihood. As the name suggests, The initialize method initializes the internal state of the process. This specially important for processes with memory, e.g. Markov. random and likelihood have the same functionality as in PDF and CPDF objects which respectively are sampling one random variable and calculating the likelihood of one random variable. This similarity is not surprising as processes are also models of probability distribution but for sequences.
Simulating data from a SSM model is equivalent to sampling from the associated stochastic process. One may sequentially use random method of the process object to simulate sequence of data. However, all process objects in ssmkit provide a random_n(n) method that returns a sequence of n samples from the process:
As our ssm_proc is of class Hierarchical, its random variable type Hierarchical::TrandomVAR which is the output of random method is a std::tuple of the random variables of each layer. The method random_n(n) returns a std::vector of length n that contains the sequence of samples, i.e. \((\mathbf{x}_1, \mathbf{z}_1), \cdots\). If you like, you can copy the \(\mathbf{x}_1, \cdots \mathbf{x}_{100}\) and \(\mathbf{z}_1, \cdots \mathbf{z}_{100}\) to separate vectors using some pure standard C++:
Note that all the statement <typename std::tuple_element<0,decltype(data)::value_type>::type> is to tell the compiler what is the type of state variable. We know it is ama::vec because we have constructed the process. But the above code is generic and can be used always even when you don't know what is the type of variables in the process!
There are a number of state estimation tools are under the namespace of ssmkit::filter. In practice state estimation filters are model-based. That means they are build having in mind particular type of SSM. Using this fact in 'ssmkit' process objects are used to define filters. Each filter may particularly be useful for some specific type of process models. This is statically checked and your code will not compile if you try to make a filter object with wrong SSM model.
The constant velocity model we defined in this tutorial is a case of famous linear Gaussian model that classical Kalman filter has been designed for. We can make a Kalman filter easily for our model:
This makes an object of class ssmkit::filter::Kalman. All the parameters of Kalman filter are read from provided process argument. ssmkit::filter::Kalman is a special case of recursive Bayesian filter where for each measurement two step of prediction on correction are applied.
Let apply Kalman filter on our simulated data. Although ssmkit::filter::Kalman provides all the low level predict() and correct() methods, it is easier to use just the filter() method for that apply the filtering on a sequence and return the result:
The output x_seq_est is a vector whose length is z_seq.size()+1 because filter() method also returns the estimate of initial state. Each element of x_seq_est is a tuple containing mean and covariance of the estimated state.
Finally, one may like to calculate the Mean Squared Error (MSE) of the Kalman filter output with respect to original state sequence. For now lets do it using standard C++: