Markov< TPDF, TParamMap, TInitialPDF > Class Template Reference

A first-order Markov process. More...

Public Member Functions
	Markov (distribution::Conditional< TPDF, TParamMap > cpdf, TInitialPDF init_pdf)
	Constructor. More...
auto	initialize () -> decltype(std::declval< TPDF >().random())
	initialize process More...
template<typename... Args>
auto	random (const Args &...args) -> decltype(std::declval< TPDF >().random())
	Sample from process. More...
template<typename... Args>
double	likelihood (const decltype(std::declval< TPDF >().random())&rv, const Args &...args)
	Calculate likelihood. More...
distribution::Conditional < TPDF, TParamMap > &	getCPDF ()
	Returns a reference to internal CPDF. More...
TInitialPDF &	getInitialPDF ()
	Returns a reference to initial PDF. More...
Public Member Functions inherited from BaseProcess< Markov< TPDF, TParamMap, TInitialPDF > >
decltype(auto)	random_n (const size_t &n, const TArgs &...args)

Detailed Description

template<typename TPDF, typename TParamMap, typename TInitialPDF>
class ssmkit::process::Markov< TPDF, TParamMap, TInitialPDF >

A first-order Markov process.

Implementation of markov process defined using initial PDF \(p(\mathbf{x}_0)\) and state transition PDF \(p(\mathbf{x}_k|\mathbf{x}_{k-1}, y^1_k, \cdots, y^N_k)\)

Dynamic Bayesian Network model of Markov process

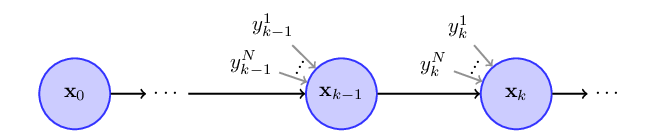
Definition at line 28 of file markov.hpp.

Constructor & Destructor Documentation

Markov ( distribution::Conditional< TPDF, TParamMap >  cpdf, TInitialPDF  init_pdf  )

inline

Constructor.

The process is constructed from an initial PDF (init_pdf) and a distribution::Conditional PDF (cpdf). The first condition variable of cpdf is used to connect the time slices, i.e. If cpdf is \(p(\mathbf{x_k}|y_0, \cdots, y_N)\) then \(\mathbf{x_{k-1}}\) is passed to \(y_0\) for random() sampling likelihood() calculation. The rest of condition variables ( \(y_1, \cdots, y_N\)) are disposed to the interface of random() and likelihood() methods.

Note

use makeMarkov builder for convenient template argument deduction

Parameters

init_pdf	Initial probability distribution \(p(\mathbf{x}_0)\)
cpdf	distribution::Conditional PDF characterizing inter time-slice dependency \(p(\mathbf{x}_k|\mathbf{x}_{k-1}, y^1_k, \cdots, y^N_k)\)

Precondition

init_pdf should provide random and likelihood methods.

The type of the random variable and the first condition variable of cpdf should be the same. The cpdf should have at least one condition variable.

Definition at line 49 of file markov.hpp.

Member Function Documentation

auto initialize ( ) -> decltype(std::declval<TPDF>().random())

inline

initialize process

Samples initial random variable \(\mathbf{x}_0\) and stores it internally.

Returns

Initial random variable \(\mathbf{x}_0\).

Side Effects

Sets the internal state to \(\mathbf{x}_0\).

Definition at line 61 of file markov.hpp.

auto random ( const Args &...  args ) -> decltype(std::declval<TPDF>().random())

inline

Sample from process.

Samples one random variable \(\mathbf{x}_k\) from the process and stores it internally.

Parameters

args	... Process condition (control) variables ( \(y^1_k, \cdots, y^N_k\)) if any.

Returns

Random variable \(\mathbf{x}_k\).

Side Effects

Sets the internal state to \(\mathbf{x}_k\).

Definition at line 76 of file markov.hpp.

double likelihood ( const decltype(std::declval< TPDF >().random())&  rv, const Args &...  args  )

inline

Calculate likelihood.

Calculate the likelihood of one random variable \(p(\mathbf{x}_k|\mathbf{x}_{k-1}, y^1_k, \cdots, y^N_k)\).

Parameters

rv	The random variable \(\mathbf{x}_k\).
args	... Process condition (control) variables ( \(y^1_k, \cdots, y^N_k\)) if any.

Returns

The likelihood of random variable \(\mathbf{x}_k\).

Definition at line 91 of file markov.hpp.

distribution::Conditional<TPDF, TParamMap>& getCPDF ( )

inline

Returns a reference to internal CPDF.

Definition at line 97 of file markov.hpp.

TInitialPDF& getInitialPDF ( )

inline

Returns a reference to initial PDF.

Definition at line 101 of file markov.hpp.

---

The documentation for this class was generated from the following file:

• src/ssmkit/process/markov.hpp